Una de las cosas que me atrajo a las ciencias es el hecho de que la ciencia no es sobre lo conocido, sino sobre lo que es todavía desconocido. No es sobre el saber, sino sobre el no saber. Cuando uno se enfrenta a un fenómeno, lo que observamos es objeto de reflexión. Cuando uno se enfrenta a lo que no se conoce, existe esa sensación de que es permitido pensar cualquier cosa, se puede explicar un fenómeno o simplemente nos permite entender.

Hace un par de días, estaba jugando con un juguete mecánico a cuerda como este:

Simplemente le daba cuerda al máximo, lo colocaba en un mismo lugar en la mesa, en el centro, y lo dejaba moverse hasta que su cuerda se acabara. Después de hacerlo muchas veces, observé y me dí cuenta de que el juguete tiende más a moverse hacia el lado derecho. Repetí más veces, y obtuve un resultado similar. Es decir, de 10 veces terminaba 7 a la derecha, y el resto a la izquierda. Me pregunté ¿Será que realmente tiende a moverse más a la derecha? a partir de mi observación, pareciera que sí, pero ¿será mi observación suficiente para llegar a esa conclusión?

Hay que probarlo de alguna manera. Con una prueba me refiero a alguna forma de demostrar de que lo que propongo puede ser cierto. Para decir que el juguete se mueve más a la derecha, y que esto tenga algo de validez más allá de mi observación, se requiere algo más riguroso, más universal. Si repitiera esta prueba mil veces, ¿la observación sería siempre la misma? que tal 2 mil veces, que tal si lo hace otra persona en otro lugar. Pero si repito y repito más veces, ¿Será siempre el mismo resultado?

Tomé un tape eléctrico y marqué el centro de la mesa con una línea. Tomé el juguete, le di cuerda hasta el final, lo puse en el centro de la mesa, en un punto exacto, y lo dejé corriendo hasta que se le acabara la cuerda.  Repetí esto 26 veces, y anoté el resultado. En la foto muestro 8 “corridas” del juguete,

Al final del experimento terminamos con un conjunto de observaciones. Unas terminaron a la derecha y otras a la izquierda. Nuestro conjunto lo voy a llamar A, y se ve algo como esto:

En total hay 17 observaciones der y 9 observaciones izq. La secuencia en la que ocurren las observaciones es la que se ve en el conjunto A. No nos interesa el orden en el que ocurrieron, simplemente cuántos hay de cada uno.

Bien, ya tenemos datos. La pregunta es ¿Cómo se puede demostrar que efectivamente el juguete tiende a moverse más hacia la derecha? Pensemos esto de otra manera, ¿Qué significa que no se moviera más veces a la izquierda? ¿Significa que el juguete se mueve de igual manera a la izquierda y a la derecha?. 

Lo primero, si, el juguete se mueve aleatoriamente, el resultado esperado serían, de los 26 movimientos, 13 izq y 13 der. Este conocimiento es importante, y viene puramente del razonamiento y de lo que sabemos sobre números y conjuntos. Dos conjuntos son iguales, si tienen el mismo número de elementos. Esto nos da un punto de inicio para demostrar si lo que observamos está cerca o lejos de ser mitad y mitad. Es decir, lo que vamos a probar es la siguiente hipótesis lógica: Si el objeto tiende a moverse más veces a la derecha, y si repito el experimento muchas veces, debería alejarse de el resultado mitad y mitad.

Debemos entonces construir un caso base, para falsificarlo, o mejor dicho para ver si no es cierto. El caso base es un conjunto de observaciones donde izq o der ocurren con la misma probabilidad, esto porque es mucho más sencillo simular esta situación, sin necesidad de usar el juguete. Que tal entonces si simplemente generamos un conjunto aleatorio de izq y der, y así podemos hacer unas 10 mil simulaciones de conjuntos de 26 izq y der. Es como hacer 10 mil veces el experimento con 26 corridas, pero esta vez al azar donde sabemos que tanto izq como der ocurren con la misma probabilidad. Luego de hacerlo, se vería algo como esto:

En la imágen solo muestro 100 repeticiones de las 10 mil que hice. Cada fila tiene 26 elementos que fueron generados de forma aleatoria en una computadora. Los ordeno izq (azules) y der (negros). En principio, dado que hay igual probabilidad de ocurrencia de izq o der, deberían ocurrir en promedio 13 veces izq y 13 veces der, pero, no siempre es así al haber sido generados aleatoriamente. Nos interesa saber exactamente de las simulaciones, cuántos a la izquierda y derecha realmente ocurren, y para eso los acomodamos en un gráfico que se le conoce como histograma:

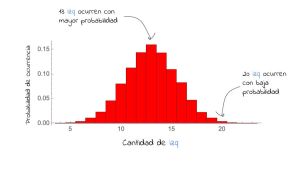
En el eje X del gráfico, tenemos las ocurrencias de izq, y en él Y, la probabilidad de que ese número de izq ocurra. Por ejemplo, hay una baja probabilidad de que, si izq y der ocurren completamente al azar, ocurran 20 izq en 26 corridas del juguete.

En el eje Y tenemos las probabilidades, es decir, la probabilidad de que ocurran en un conjunto 13 izq, que es la mitad, es de 0.15 aproximadamente. Este gráfico es bastante revelador. Lo primero es, que si repetimos un experimento muchas veces, comienza a emerger la forma de una curva muy particular. A esta curva se le conoce como la Campana de Gauss (curva distribución normal en estadística). Lo segundo, es que la probabilidad de que todos los elementos en una corrida sean izq, o todos der, si esto ocurre completamente al azar, es extremadamente baja, casi 0.

Lo que nos queda ahora es ver donde calza nuestra observación del experimento inicial, de el real,  dentro de este histograma. Recordemos que son 26 observaciones de las cuales 17 son der y 9 izq. En el histograma lo marco en azul,

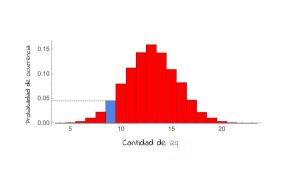
Como leemos esto:  si el juguete se moviera a la izq o der de forma completamente aleatoria, sin tendencia a moverse más a un lado que a otro, lo que observamos en nuestro experimento real, ocurriría con una probabilidad menor a 0,05. Con esta información, ¿podemos decir que el juguete se mueve más a la izquierda o a la derecha?  si y no, depende de qué probabilidad aceptamos como muy baja en ese histograma, pareciera. Lo que sí nos dice es que parece alejarse del resultado más esperado si fuera completamente aleatorio. Lo que nosotros observamos parece no ser común, si el juguete fuera aleatorio. Para dar una conclusión definitiva, tendríamos que establecer alguna regla o punto de corte en ese histograma, donde aceptamos que la probabilidad de ocurrencia de una situación, por ejemplo menor a 9 izq, es tan baja que se aleja demasiado de un comportamiento aleatorio. Eso es lo que se hace en ciencias, se le conoce como prueba de hipótesis estadística, pero en alguna otra columna lo explico con más detalle.

Por supuesto que este es un ejemplo sencillo de un proceso de razonamiento científico, la realidad presenta mucho más dificultades, y cómo ven las conclusiones incluyen “incertidumbre”, donde solamente podemos determinar que tan probable es nuestro resultado, pero no una respuesta absoluta. Qué conclusiones sacamos de este ejercicio:

1. Que los experimentos debe ser repetidos muchas veces
2. Que se necesita un marco estadístico de referencia para poder sacar conclusiones a partir de observaciones
3. Utilizamos el azar como marco de referencia. En principio cualquier observación que muestra un patrón muy marcado, este patrón se aleja de lo aleatorio.
4. Los fenómenos que observamos generan distribuciones estadísticas, las cuales podemos utilizar para determinar, si un patrón es diferente a aleatorio
5. Que los experimentos tienen incertidumbre, y que las conclusiones a veces no son tan claras, deben ser manejadas con cuidado.

En este ejercicio de pensamiento científico, jugamos, observamos, repetimos, preguntamos, propusimos, experimentamos, obtuvimos datos. Razonamos, planteamos una hipótesis, calculamos probabilidades, hicimos un histograma, falsificamos y obtuvimos una conclusión rigurosa y universal. Eso es el pensamiento científico.

Tomás de Camino Beck, Ph.D

Escuela de Sistemas inteligentes

Universidad CENFOTEC