Prácticamente todas las tecnologías que hoy utilizamos, tienen una base matemática. La tienen no porque esté prescrito, sino porque es el pensamiento, la mecánica, la que nos permite razonar de forma exacta y enfrentar problemas de manera mucho más precisa. Todos y todas pensamos de alguna manera matemáticamente. Debemos dejar de pensar en la matemáticas como algo que sé o no sé, o no somos buenos, sino como algo que me permite formalizar el pensamiento y desarrollar ideas. La matemática se descubre y redescubre de forma personal.  También se diseña y se inventa.  

En la columna de esta semana quiero llevarlos por esa aventura del pensamiento matemático y cómo se desarrollan ideas a través de la matemática, partiendo de la formalización de un concepto que todos entendemos como la “sorpresa”, ¿podemos medir la sorpresa?.

Algo nos “sorprende” cuando no lo esperamos, es decir, dentro de las posibilidades de que algo en particular ocurra, esa posibilidad es baja, y claro, cuando ocurre nos parece una sorpresa. Veamos con el siguiente ejemplo: Supongamos que lanzamos una moneda cuatro veces y obtenemos el siguiente resultado:

Vemos que siempre sale “corona”. Nuestra expectativa, entonces, es que la próxima vez que sea lanzada probablemente va a salir corona nuevamente.  Si cayera escudo, nos sorprendería mucho más que si cae otra vez corona. 

Allí mencioné la palabra “probabilidad”. Probabilidad es un concepto al que estamos expuestos diariamente, y tenemos cierta intuición de lo que es.  Cuando lanzamos una moneda, sabemos que no hay seguridad alguna de que la moneda caiga corona o escudo (cara o sello).  Al haber incertidumbre en el resultado, lo mejor es expresarlo como una probabilidad así, en una moneda que tiene dos caras, sabemos entonces que hay una probabilidad 1 de 2, es decir 0.5 de que sea escudo, y 0.5 que sea corona.  Informalmente, la probabilidad describe la posibilidad de que un evento ocurra en términos de un valor entre 0 y 1.  Lo podemos pensar también como porcentaje,  así la moneda al lanzarla puede caer 50% de la veces escudo y el otro 50% corona.

Ahora bien, la “sorpresa” es “al revés” de la probabilidad, es inversa, a mayor probabilidad de que algo ocurra, mucho menos la sorpresa. Acá voy a meter algo de fórmulas, pero nada complicado, paciencia.  La sorpresa la podríamos medir entonces de la siguiente manera:

 

Así por ejemplo en el caso de la moneda, la sorpresa de escudo sería 1 / 0.5 = 2, y exactamente igual para corona.  A medida que la probabilidad sea menor, digamos que sea una moneda injusta, la sorpresa será cada vez más alta. Ahora bien, podemos mejorar nuestra fórmula de sorpresa, pues tiene un problema. Veamos la siguiente situación,

Si lanzo la moneda 10 veces, y cae siempre corona,  la sorpresa de que caiga otra vez corona, debería ser 0, en nuestra fórmula no lo es (de hecho es 1).  Para eso podemos utilizar un truco.  Cambiemos nuestra fórmula de la siguiente manera,

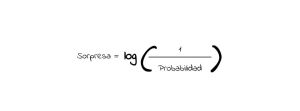
Noten como ahora aplico el logaritmo a la fórmula.  En una columna futura hablaré de logaritmos, por ahora la ventaja es que el logaritmo de 1 es 0, esto significa que si la probabilidad de que siempre caiga corona es 1, entonces la sorpresa va a ser 0, y si la probabilidad de escudo es 0, está fórmula nos da indefinido, lo cual está bien, pues no tiene sentido calcular la sorpresa de algo que nunca ocurre. Para explicarlo mejor, veamos la figura,

A medida que aumenta la probabilidad de que algo ocurra, menor será la sorpresa, y si algo ocurre con probabilidad 1, la sorpresa será 0. Si tenemos una moneda que de 100 veces cae 80 veces escudo y 20 corona,

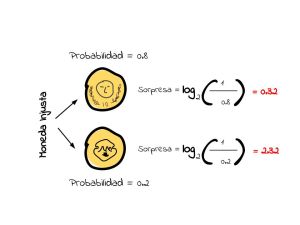
vemos que hay más sorpresa que caiga escudo. Ahora lo interesante es que podemos calcular la sorpresa de una secuencia de lanzamientos, por ejemplo escudo-corona-escudo, simplemente sumando la sorpresa individual ¿alguien se anima a explicar por qué?,

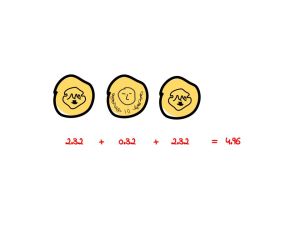
es decir la sorpresa de esa secuencia es 4.96.

Ahora sí viene lo más interesante. Si queremos calcular qué tan sorprendidos en general estaríamos si lanzamos la moneda 100 veces, lo hacemos de la siguiente manera,

 

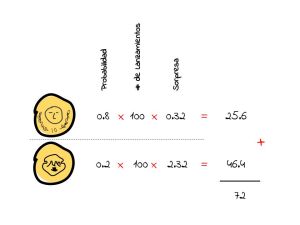
La sorpresa total que tendríamos sería de 72.  Por sí solo este número puede que no signifique mucho, pero lo podemos usar para comparar diferentes situaciones o contextos de lanzamiento de monedas.  Así por ejemplo si la probabilidad de corona es 0.9 y la de escudo es 0.1, la sorpresa total de 100 lanzamientos sería de 46.7, es decir esta última situación nos daría menos sorpresas.

Bueno y que tiene que ver la entropía en todo esto.  Resulta ser que si en lugar del total de sorpresa (72 en nuestro ejemplo con 100 lanzamientos), calculamos el “promedio” de sorpresa, que es 72 dividido entre 100 lanzamientos que nos da 0.72, esa es la entropía. Dicho de otro modo, la entropía es la sorpresa promedio,o mejor dicho, la sorpresa esperada cada vez que lanzamos la moneda es de 0.72.  La entropía es un concepto extremadamente poderoso que ha aparecido en física, química, biología y en teoría de la información, pero hablaré de este concepto en una columna futura.

¿Qué relevancia tiene el cálculo de la sorpresa y la entropía?, piensen grande. Resulta ser que en ciencia de datos, estos valores sirven para clasificación de grupos de datos o para determinar la similaridad de información entre dos procesos, pues permite cuantificar qué tan diferentes son dos conjuntos de datos. También en la toma de decisiones es valioso, pues nuestras decisiones deberían apuntar a minimizar el grado de sorpresa, o incluso lo contrario, por ejemplo en innovación de productos,  introducir alguna estrategia que garantice un alto grado de sorpresa cuando se introduce un producto en el mercado. 

Para aquellos más afines a las matemáticas les dejo este reto, ¿cómo es que la sorpresa promedio es igual a la entropía? (ojalá compartan en comentarios).

Última cosa, algunas de mis columnas serán este tipo de exploraciones, tal vez no sean tan populares, pero la intención es la de mostrar cómo se van construyendo conceptos matemáticos, y estimular a lectores y lectoras a que exploren más las matemáticas, preguntándose el por qué… 

Dr. Tomás de Camino Beck,

Director de la Escuela de Sistemas Inteligentes

Universidad Cenfotec