Hoy en día es casi parte del vocabulario de todos y todas hablar de análisis o analítica de datos. Lo es porque los datos han pasado de ser una especie de abstracción, a algo que podemos percibir, algo casi tangible. Casi que todos y todas estamos claros que nosotros mismos somos datos en un mundo donde todo es digital.

La realidad es que los datos por sí solos no son interesantes. Los datos se transforman en algo valioso, cuando los relacionamos con la dinámica de los sistemas reales, cuando los relacionamos con algún fenómeno que queremos entender y explicar o predecir.  Más aún, cuando decimos que hacemos análisis o analítica de datos, no es simplemente poner unos datos en una tabla de Excel o Sheets y graficarlos, con alguna estadística descriptiva; analítica de datos significa poder establecer una conexión entre los datos y un modelo matemático o estadístico que es la base formal de un fenómeno. 

 

Uno de esos modelos de gran utilidad para extraer información de datos, y que deberían tener presente en su “caja de herramientas”, se le conoce como Simulaciones de Monte Carlo, un algoritmo o concepto estadístico, bastante sencillo pero muy poderoso, y de eso hablaré esta semana. Comenzaré explicando un ejemplo sencillo, y luego haré un ejemplo más avanzado calculando algunas cosas de la epidemia de COVID en Costa Rica.

Ejemplo sencillo

Supongamos que queremos calcular el área de Costa Rica en un mapa (tomada de Wikipedia).

 

Como el mapa es una imagen con píxeles, para calcular el área, podríamos contar el número de píxeles del mapa, y conociendo el área de un pixel, estimar el área total. Para eso podemos filtrar el mapa superior, para generar uno de dos colores como el siguiente,

 

y ahora simplemente cuento el número de píxeles blancos y listo. En total en este mapa, tenemos 51,123 píxeles blancos, y cada píxel es de 1 kilómetro cuadrado. 

Nada nuevo por el momento. En realidad no ocupamos contar todos los píxeles, podemos tomar una muestra para poder aproximar el área. Intuitivamente sabemos, que el área blanca, ocupa una proporción del total de la imagen, y que si seleccionamos al azar un punto cualquiera, tiene una probabilidad de caer en el área blanca que es proporcional al espacio que ocupa en toda la imagen. Acá lo muestro con una simulación,

En la simulación se van escogiendo puntos al azar (rojos cuando caen en el mapa y blancos cuando caen afuera), y en la parte de abajo se muestran cuantos puntos se escogen, y la proporción que cae en el área blanca.  Si lo dejan correr por algún tiempo, a partir de los 1000 puntos al azar comienza a llegar a una proporción estable, que es aproximadamente 31%.  Entonces, si la imagen total tiene un área de 160,000 kilómetros cuadrados, el área estimada de Costa Rica, utilizando una muestra aleatoria, sería de 49,600.  Dado que estamos tomando puntos al azar, podemos repetir muchas veces esta simulación, hasta llegar a unos 1500 puntos de muestra, y obtenemos el siguiente resultado,

 

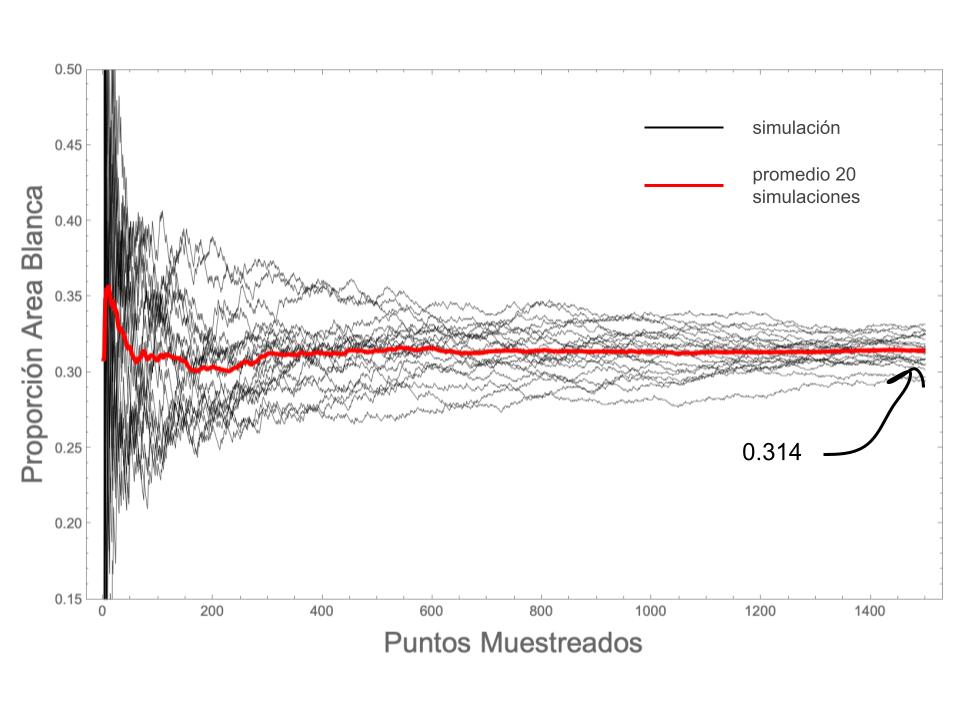
El promedio de 20 simulaciones es de 0.314, lo que significa un área de Costa Rica que estaría entre 47,040 y 53,120 kilómetros cuadrados, con un promedio de 50,296, que no está muy lejos del real.

Ustedes dirán, ¿y para qué hacer un muestreo cuando conozco el valor real? Lo haríamos porque muchas veces no podemos estimar el valor real y necesitamos aproximarlo. Este ejemplo lo utilizo simplemente para mostrar cómo un muestreo aleatorio, y conociendo algo el sistema que se estudia (la proporcionalidad de las áreas), se puede aproximar información de un sistema más complejo.

En el ejemplo del área, lo que se hace es calcular una integral usando este método, pero ahora un ejemplo algo más complejo, un ejemplo con los datos de la pandemia COVID Costa Rica. 

Una aplicación a los datos COVID

Durante la epidemia de COVID, se reportaron nuevos casos, casos activos, personas hospitalizadas, fallecidas, entre otras, diariamente. La analítica de datos, utilizando estos datos, consistía en poder determinar la duración y el impacto de una ola epidémica, poder predecir ocupación hospitalaria, determinar impacto de medidas, vacunación y muchas otras cosas pertinentes al manejo de epidemias.

Para entender aspectos de dinámica de contagio y probabilidad de infección, los datos de personas “activas” con la enfermedad es de mucha utilidad, y estos eran reportados diariamente. Las personas activas, son las personas que sospechaban tener COVID, se acercaban a algún centro de salud, se les aplicaba una prueba de COVID, y se registraba como persona enferma.  A esta persona se le imponía una cuarentena por un número determinado de días, y luego se daba de “alta” ya sea aplicando una prueba de confirmación o no. Durante todo este período a la persona se le consideraba “activa”.  

¿Porqué utilizar casos activos? Los casos activos dan una buena representación de la dinámica de la enfermedad, pues indican cuántas personas están enfermas cada día, y por tanto si la dinámica de contagio crece, decrece, y a que razón lo hace.

En Costa Rica se reportaban diariamente los casos activos, desde inicios de la pandemia, hasta el 30 de mayo del 2022.  La siguiente gráfica muestra los datos,

 

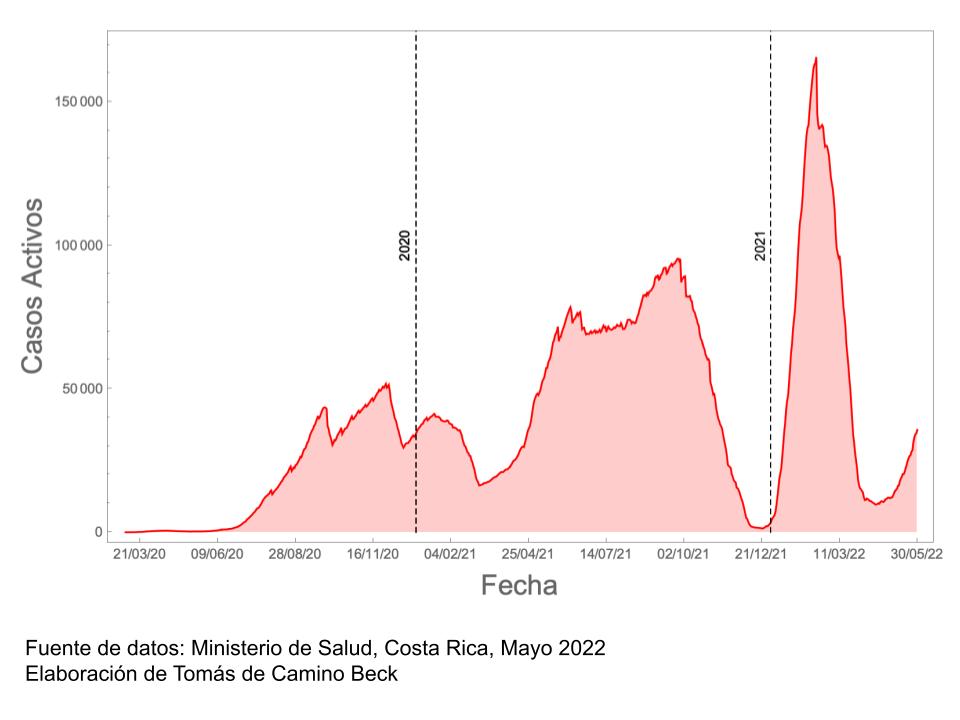
Al observar la primera gran ola epidémica (junio 2020 a febrero 2021), se comenzó a notar algo en los datos de casos activos, que no correspondía a lo esperado en la dinámica de epidemias (lo que yo llamo la cabeza de Bart Simpson).  Vean por ejemplo el gráfico sólo de mayo, junio y julio del 2020,

 

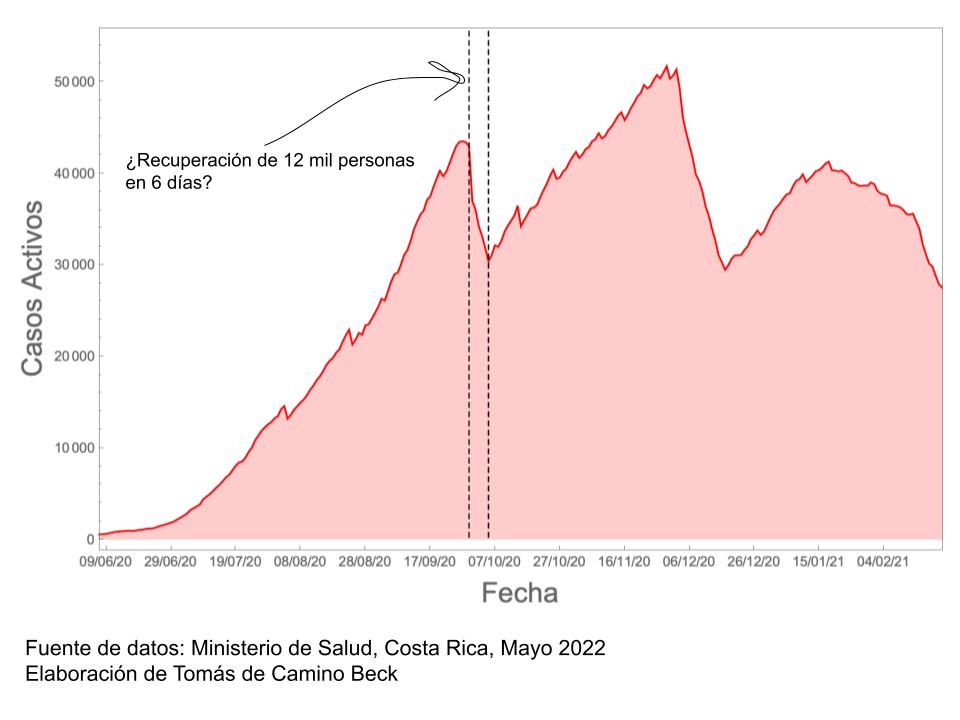
Se observan caídas en el número de activos en muy poco tiempo (más de 12 mil personas recuperadas en unos cuantos días), esto claramente no se debe a la dinámica de la enfermedad sino probablemente a otras razones. La explicación posible es que la certificación o dar de alta a una persona en cuarentena, o por lo menos en el registro de los datos, estaba atrasada. Dicho de otro modo, lo observado en los datos, corresponde a un atraso administrativo, y no a algo que corresponde a la dinámica de la enfermedad. 

Indiferentemente de los problemas de administración de salud, tener la información de casos activos es vital.  ¿Hay otra forma de calcular cuántos activos realmente habría?, acá es donde viene la Simulación de Monte Carlo.

De COVID, sabemos que una persona en promedio se recupera en unos 14 días (con algunas variantes).  Otra cosa que sabemos es que diferentes personas, permanecen con COVID diferentes períodos de tiempo.  Esta variabilidad se captura en lo que se llama una distribución de Poisson (LINK: https://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson).  Es decir, la probabilidad de que una persona se recupere, en un tiempo determinado, viene dado por esta curva,

 

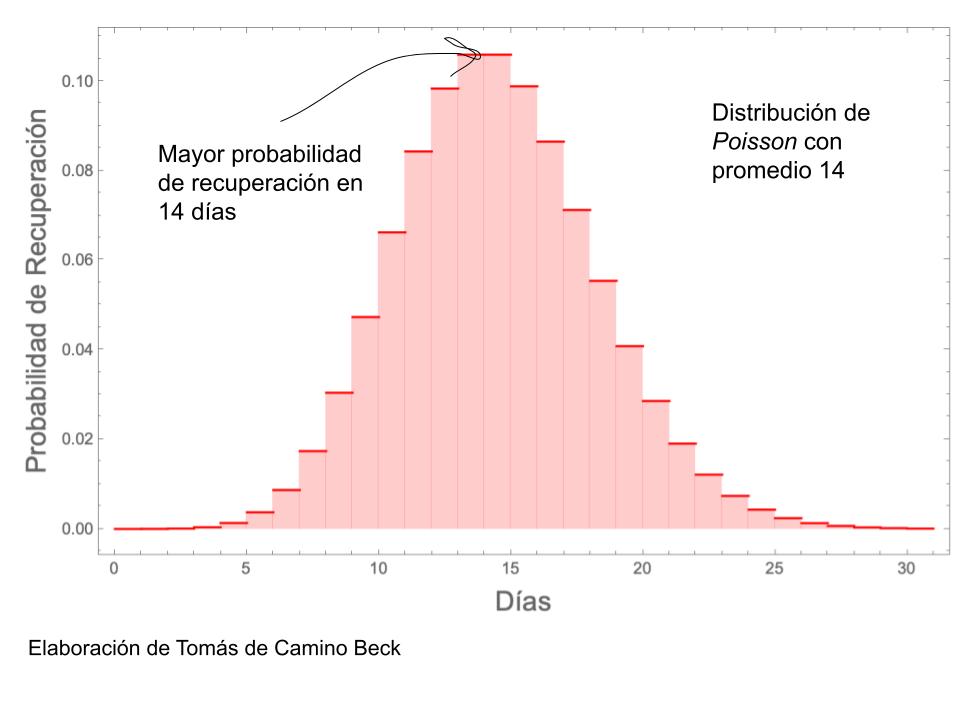
La curva anterior nos indica la probabilidad de una persona en recuperarse en un número determinado de días. Como ven, recuperarse en 5 días es poco probable, así como una recuperación de mayor de 25 días.  Lo más probable es recuperarse en 14 días.  El hecho de que utilicemos esta distribución, obedece a lo que sabemos de dinámica de enfermedades y de algunas estimaciones específicas para COVID.  Ahora entonces lo que trataremos de hacer es, a partir de los nuevos casos de COVID reportados diarios, simular su recuperación, persona a persona, para luego compararlo con lo reportado de casos activos.

Utilizando MonteCarlo y la Distribución de Poisson, lo que hacemos es “simular” cuántos días cada persona nueva, según los datos diarios, permanece como caso activo, y recalcular a partir de allí todos los casos activos. De manera muy similar a la idea del mapa, utilizando números aleatorios hacemos ese cálculo que describo en la siguiente figura,

 

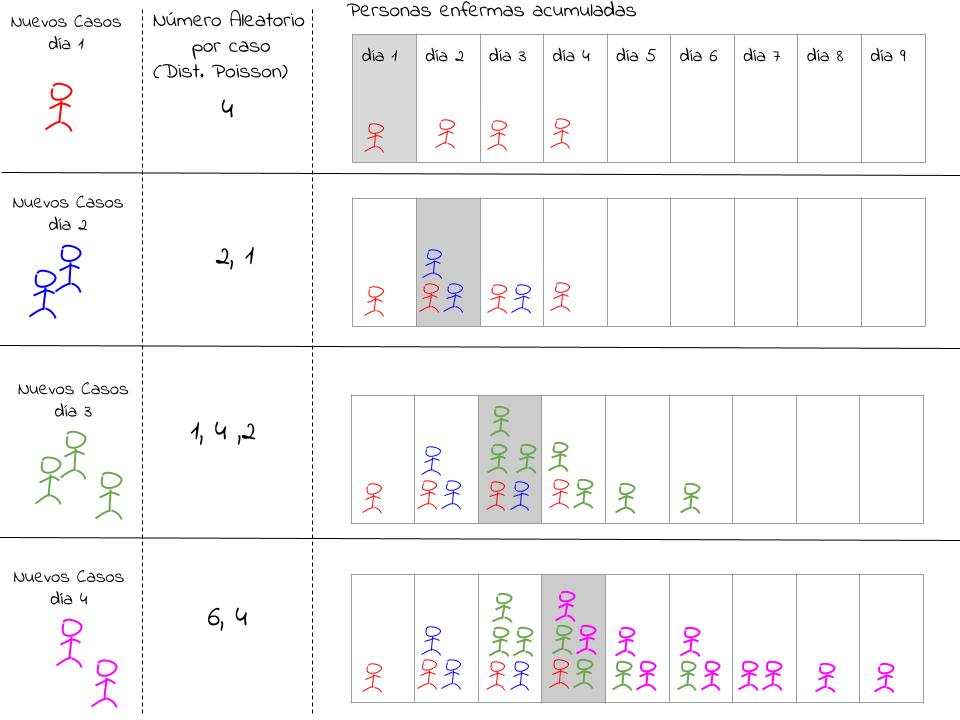
Para cada caso nuevo que se registra por día, se proyecta, utilizando Monte Carlo, cuantos días estaría como caso activo en el futuro, y se agrega a nuestra lista proyectada de activos.  De esa manera se van acumulando los casos activos como se muestra en el diagrama.

El resultado de la simulación comparado con  los datos reportados de casos activos,  se pueden ver en la siguiente gráfica,

 

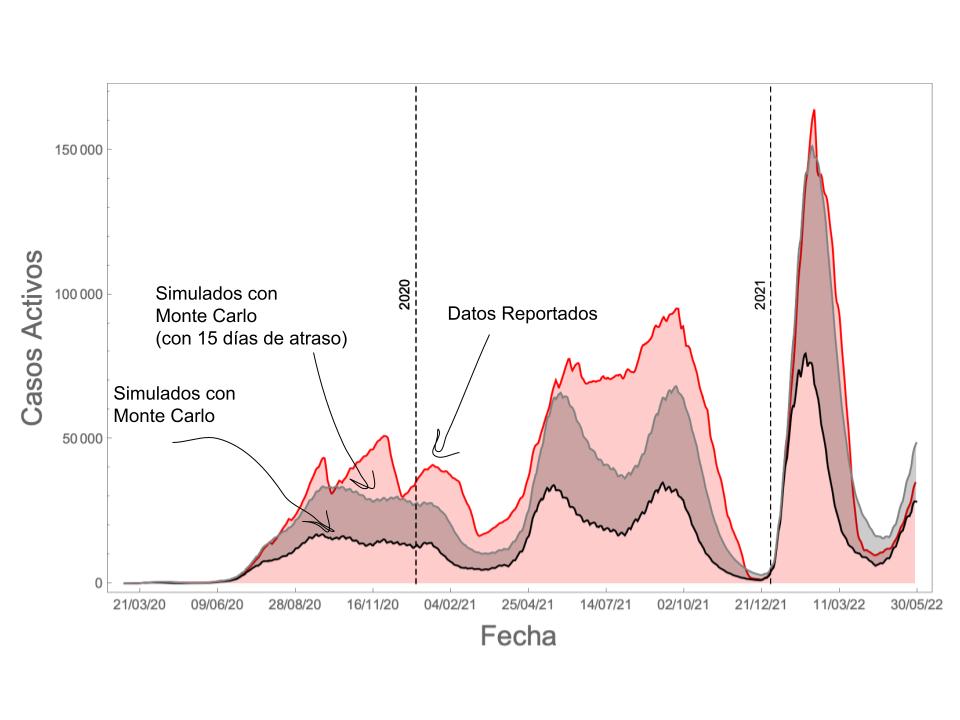
Noten como el total de casos activos (línea negra) debería ser mucho menor al reportado (línea roja).  La línea gris los simula además con 15 días en el atraso de certificar recuperados, lo cual nos indica el tiempo de retraso en la certificación de recuperados.  Sin entrar en detalles con respecto al manejo de la pandemia (que no es la intención de la columna esta semana), se observa un claro atraso en la certificación de casos activos, y que la forma de la curva no registra la dinámica real de la enfermedad, pero por suerte, esta se puede estimar con Simulación de Monte Carlo.

¿Por qué es importante hacer estas estimaciones de casos activos? Porque de la buena estimación de estos casos, se pueden determinar acciones de control, estimar si tienen efecto o no, cuándo y cuáles se deben aplicar, y también se puede dar una estimación de incapacidades e impacto laboral.

Comentarios finales

Primero, me disculpan lo extenso de la columna de esta semana y todos los cálculos y gráficos para el ejemplo de COVID los realice con Wolfram Mathematica, utilizando los datos publicados por el Ministerio de Salud.

A este tipo de estimaciones numéricas, se le conoce como Simulaciones de Monte Carlo. Más formalmente, es un método matemático numérico, para poder estimar posibles escenarios que tienen alta incertidumbre. Sus aplicaciones son numerosas, y hoy en día en cualquier computadora se puede implementar el algoritmo, incluso en una hoja de cálculo como Excel.

Las Simulaciones de Monte Carlo son un método muy utilizado y extremadamente práctico para aproximar problemas con alta confianza, definitivamente parte de la caja de herramientas de cualquier analista de datos.

 

Tomás de Camino Beck

Director Escuela de Sistemas Inteligentes

Universidad Cenfotec